Contents:
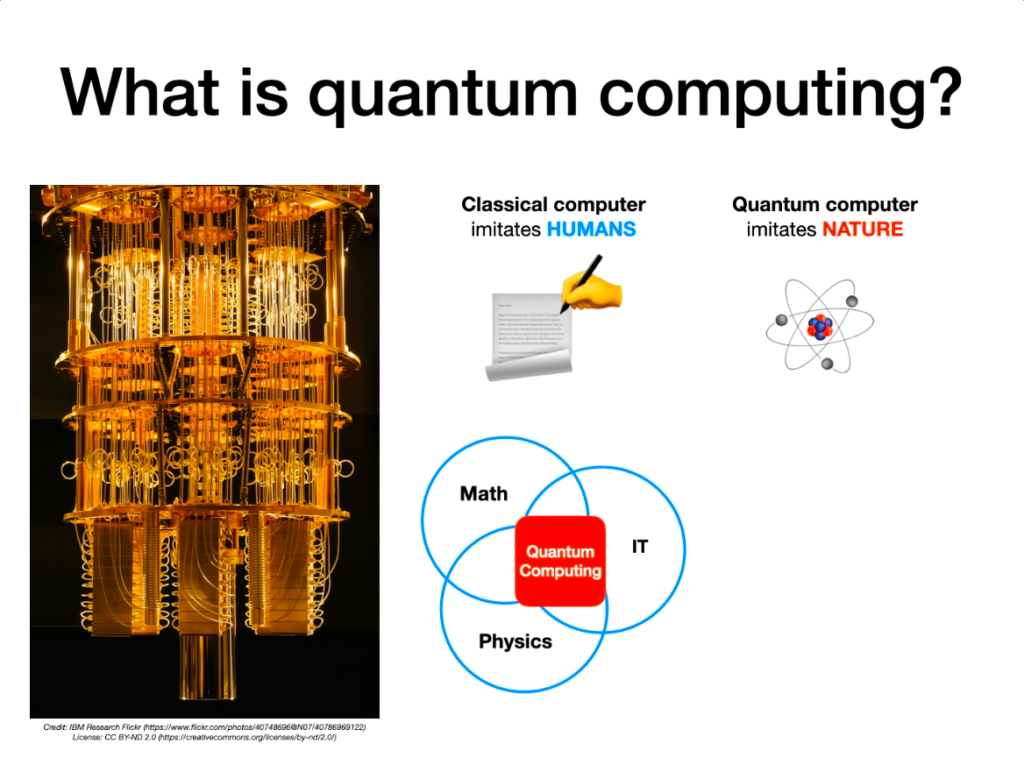
3:18 Quantum & IT
7:50 Classical vs quantum programming
12:40 The quantum world – For programmers
21:53 The qubit
35:48 General pattern (classical states / superposition / collapse)
41:12 State as a vector
56:04 Programming!
1:04:33 Environment & Interpretations
1:11:30 Quantum gates, isolation, and information
1:34:29 Quantum impracticality
ERRATUM:
The D-Wave machine is a qubit-based quantum computer. I wanted to contrast it with gate-based, universal quantum computers. Also, at “The role of information” slide, I wanted to say that the qubit collapsing to state |0> (not |1>) means that the cat survives.
ADDITIONS:
“The core idea” slide: Note that classical states are mutually exclusive, that is, according to our everyday intuition they shouldn’t co-exist simultaneously. Also, isolation is very important: quantum mechanics guarantees only that isolated physical systems can be assigned a state (vector). The quantum-state concept can be extended to include non-isolated physical systems as well (see the EPR pair below for justification), using the so-called density-matrix formalism instead of vectors, but that is out of scope for this talk.
“Entanglement – The EPR pair” slides: Quantum mechanics guarantees that every isolated system has a quantum state (vector) of its own. To make the example clearer, suppose that the EPR pair system is isolated. Then, the fact that the two individual qubits cannot have their own states implies that they are NOT isolated from each other (within the EPR-pair system). Curiously, this means that a single qubit of an EPR pair isn’t isolated but isn’t in a classical state either… the density-matrix formalism mentioned above was invented to be able to assign a quantum state even in such situations.
“Quantum gates & information” slides: We assume that before applying the gate U, the state of the environment is independent of |ψ>. So if our “detective” is only allowed to examine the environment to figure out |ψ>, then applying a quantum gate won’t help her, as she still won’t be able to correlate |ψ> with the new state of the environment (what’s more, she won’t be able to correlate |ψ’> either).