Introduction
Imagine we are given a solid ball B. The Banach-Tarski paradox is a mathematical theorem published in 1924, saying that we can split B into a finite number of disjoint parts, in a way that afterwards, by applying only translations and rotations on those parts, we finally end up with two identical copies of B. We can do all this by smartly exploiting certain counterintuitive properties of infinity.
On the basis of our physical intuition, this theorem is a scandal. To many people, such a theoretical result clearly indicates that something isn’t quite right with the axioms of mathematics. The Banach-Tarski theorem basically suggests that in the mathematical model of physical reality, we can create something out of nothing, which definitely shouldn’t be allowed, because in reality the total mass of a closed system can never increase.
How is it done?
If you are not familiar with the construction that duplicates B in the Banach-Tarski paradox, there are two excellent and easily understandable expositions you can check, here and here.
Veronese’s continuum

According to the geometry developed by Giuseppe Veronese in the 19th century, the Banach-Tarski paradox is not as devastating as it first looks. Namely, it is not the ball B that is duplicated, but only the points of B, which is not the same thing!
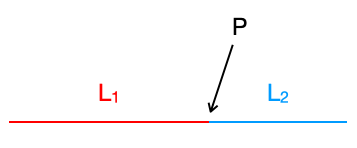
In Veronese’s geometry, the continuum, e.g. a line or a 3D solid object, isn’t equal to its points. Basically, the points can be thought of as mere labels. As an example, if we “break” a straight line segment L into two pieces, L1 and L2, and then join them up again to form L, a point P will indicate where L1 ends and L2 begins. But most importantly, P is not part of L, it only acts as kind of an abstract label that marks the boundary between L1 and L2. We can break L at infinitely many different places, each characterized by a different point. We say that these infinitely many points (i.e. labels, including the two end points) “belong to L”, or to put it differently, they are the “points of L”.
Thinking about it this way, we realize that a straight line is conceptually different from a set of points. That is, the straight line is not composed of points. As the famous mathematician Henri Poincaré once explained:
[…] there is supposed to be, between the elements of the continuum, a sort of intimate bond which makes a whole of them, in which the point is not prior to the line, but the line to the point.
Henri Poincaré
A bit more detailed introduction to Veronese’s geometry, with a list of further readings, is given here.
There is no paradox
Similarly to a straight line, a solid ball also has infinitely many points (labels) belonging to it, but those are not part of the ball. The ball isn’t composed of its points either. And in the proof of the Banach-Tarski theorem, it is merely this set of points of the ball B that is duplicated (by dividing it into a finite number of disjoint subsets in a tricky way), not the 3D ball itself.
Note 1 Strictly speaking, it is eventually the radius line segments of the ball that are duplicated in the proof, via duplicating their end points that lie on the surface. But even with that, the argument remains the same: a 3D ball is not equal to the set of its 1D radius line segments either.
I don’t say that the Banach-Tarski paradox isn’t weird. All I was trying to show here is that if we adjust our physical interpretation of geometry to be in line with Veronese’s ideas, the Banach-Tarski paradox suddenly won’t appear more scandalous than e.g. Hilbert’s Hotel, or the Hyperwebster Dictionary. It is because once we adopt this different view, the Banach-Tarski theorem isn’t anymore about duplicating a 3D object, but only a set of (non-physical) points, or labels if you will.
Conclusion
Thus, the root cause of the paradox isn’t that the Axiom of Choice is used in the proof, but rather our own way of picturing how geometric objects, like points, correspond to physical reality.
Note 2 As Veronese’s geometry allows infinitesimal magnitudes, it would be interesting to see whether the very same paradox arises if, instead of considering points, we’d split the ball into infinitesimally small 3D volumes. Since such volumes are really parts of the ball, not only labels, the argument I gave above wouldn’t work. That is to say: “Houston, we (may) have a problem.” 😉